题目分析

这个题目很奇妙，小伙伴们认真思考思考。

堆+贪心

直观的感觉应该如何去做？是不是应该先去做出现次数最多的任务。如果先做了出现次数少的B，那么剩余出现次数多的A，每两次之间都需要等待间隔n。这其实就是一种贪心思想。想看证明的小伙伴可以去Leetcode621题官方题解中查看。

因此我们可以建立一个最大堆，记录着每个字符的出现次数。n + 1个长度为一组，这个非常重要，因为A出现一次以后，下一次要等待n个单位时间，下一次A出现最早是在n + 1单位时间以后。我们从最大堆中连续拿出n + 1个数。然后再将它们数量都减1之后再放入最大堆中。当最大堆中拿出的第一个数只有最后一个时，并且堆为空，说明已经完全做完了，返回所用的时间。

算法的**时间复杂度为$O(nlog(m))$，空间复杂度为$O(m)$**，其中n为指令个数，m为指令种类，这里为大写字母，因此最大为26。

#include<iostream>
#include<vector>
#include<queue>

using namespace std;

class Solution {
public:
    int leastInterval(vector<char>& tasks, int n) {
        priority_queue<pair<int, int>> heap;
        vector<int> alpha(26);
        for (char c : tasks) alpha[c - 'A']++;
        for (int i = 0; i < 26; i++) heap.push({ alpha[i], i });
        int res = 0;
        while (heap.top().first) {
            vector<pair<int, int>> maxiChar;
            for (int i = 0; i <= n; i++) {
                if (!heap.empty() && heap.top().first) {
                    maxiChar.push_back({ heap.top().first, heap.top().second });
                    heap.pop();
                }
                else if (maxiChar[0].first == 1) return res;
                res++;
            }
            for (pair<int, int> p : maxiChar) heap.push({ p.first - 1, p.second });
        }
        return res;
    }
};

数学

数学方法太巧妙了，我这里参考了官方题解的答案。

我们先考虑执行次数最多的任务，记为A，执行次数为maxExec，而且具有相同执行次数的任务有maxCount个。不妨设有A，B，C三个任务都要执行maxExec次。那么n + 1个单位时间为一组。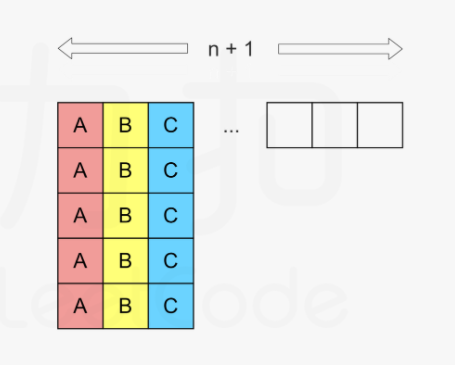

按照贪心思路，我们每次都要首先执行这3个任务，其他的时间往空余时间里面挤。不妨设n = 5，那么我们再1，2，3时间执行A，B，C，那么在4和5执行其他的任务，一定不会产生问题。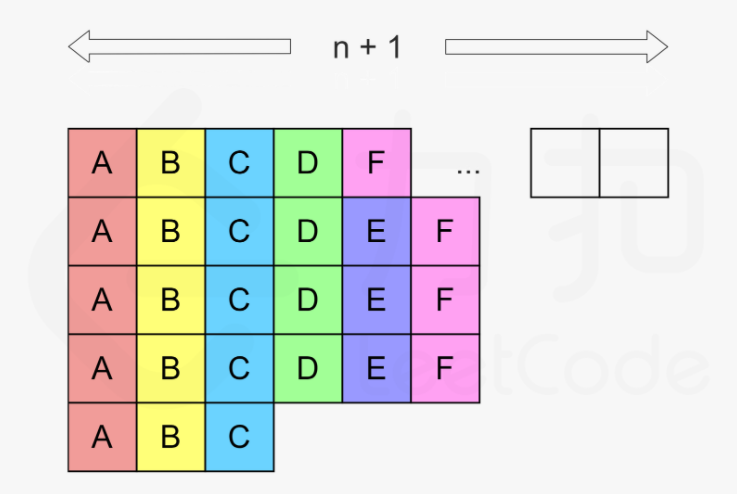

如果按照我们的想法，那么所用的时间是
$$(maxExec - 1) \times (n + 1) + maxCount$$

但是这个前提是我们不会超过n + 1列，如果maxCount > n 或者其他指令的数量nums > (maxExec - 1) x (n + 1 - maxCount)，那么就不满足上面的算法。

不满足上面的算法主要原因就是超过了n + 1列，在n + 1列中，两个相同任务之间的间隔都不少于n，因此任何两个相同操作间隔都至少为n，就是我们不需要任何待命操作，所以总执行时间就是任务总数。所以执行任务所用时间是两者的最大值。

代码非常短，但是很不容易想到，需要小伙伴们认真品味。

算法的**时间复杂度为$O(n + m)$，空间复杂度为$O(m)$**，其中n为指令个数，m为指令种类，这里为大写字母，因此最大为26。

#include<iostream>
#include<vector>
#include<unordered_map>
#include<algorithm>

using namespace std;

class Solution {
public:
    int leastInterval(vector<char>& tasks, int n) {
        unordered_map<char, int> count;
        for (char c : tasks) { count[c]++; }
        int maxExec = 0, maxCount = 0;
        for (auto x : count) {
            if (x.second > maxExec) { maxExec = x.second, maxCount = 1; }
            else if (x.second == maxExec) { maxCount++; }
        }
        return max((maxExec - 1) * (n + 1) + maxCount, int(tasks.size()));
    }
};

刷题总结

这个题目我最推荐的方法是我写的方法，堆是这类问题的通解，也是一个非常非常重要的数据结构，小伙伴们一定要会使用它。